흑기사 방랑일지 ahden's DevNote

원근 투영 변환 (Perspective Projection Transformation)

3D에서 2D 화면으로

원근 투영의 근본적인 목적을 기억하자: 우리 시야 내에 들어오는 3D 공간 상의 객체들을 2D 화면으로 맵핑시키는 것이다. 즉, 3차원을 2차원으로 변환하는 것이므로 z축은 사라진다.

그래서 ‘원칙’적으로는 일단 2D 화면으로 변환된 물체는 (z축이 사라졌기 때문에) 원래의 3D 공간으로 되돌아갈 수 없다.

뷰 공간에서 NDC 공간으로

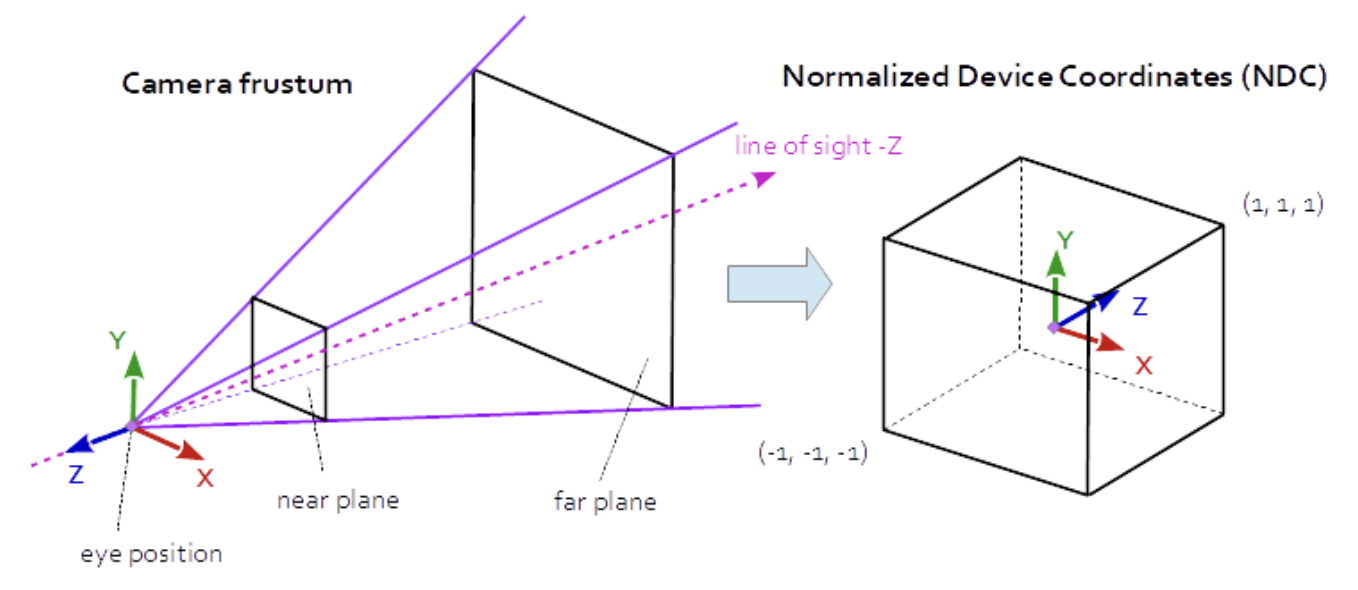
Untitled

그렇지만 실제의 원근 투영은 이렇다: 위 그림과 같이, 프러스텀 안의 모든 점들을 xyz축 요소 [-1, 1] 내의 큐브로 변환하는 것이 목표다. 그리고 이 큐브는 가로2 x 세로2 x 높이2 크기를 갖는다. (여기서 프러스텀은 시야각과 일정 z축 거리 (n, f)로 정의된다.) xyz축이 그대로 유지되는 입장에선 여전히 3D 공간에서 3D 공간으로의 변환인 것이다. 그러면 z축이 살려두는 이유는 무엇일까? 그 이유는 바로 실제 화면 픽셀에 그릴 지 버릴 지를 결정하기 위한 차폐 테스트 용도로 쓰이기 때문이다. 단순히 2D 화면으로 맵핑하기 위해서는 2D 공간으로의 변환으로 충분하지만, 일반적으로 시야에서 가려지는 물체는 화면 픽셀에 반영할 필요가 없다. 그래서 동일한 2D픽셀 위치에서 더 가까운 z값을 가진 픽셀만 일반적으로 살아남는다.

원근 투영 변환 구하기

원근 투영은 꽤 복잡해 보이지만 단계적으로 나눠서 살펴보면 생각보다 어렵지 않다:

Step 1: 시점에서 투영 평면까지의 거리 구하기

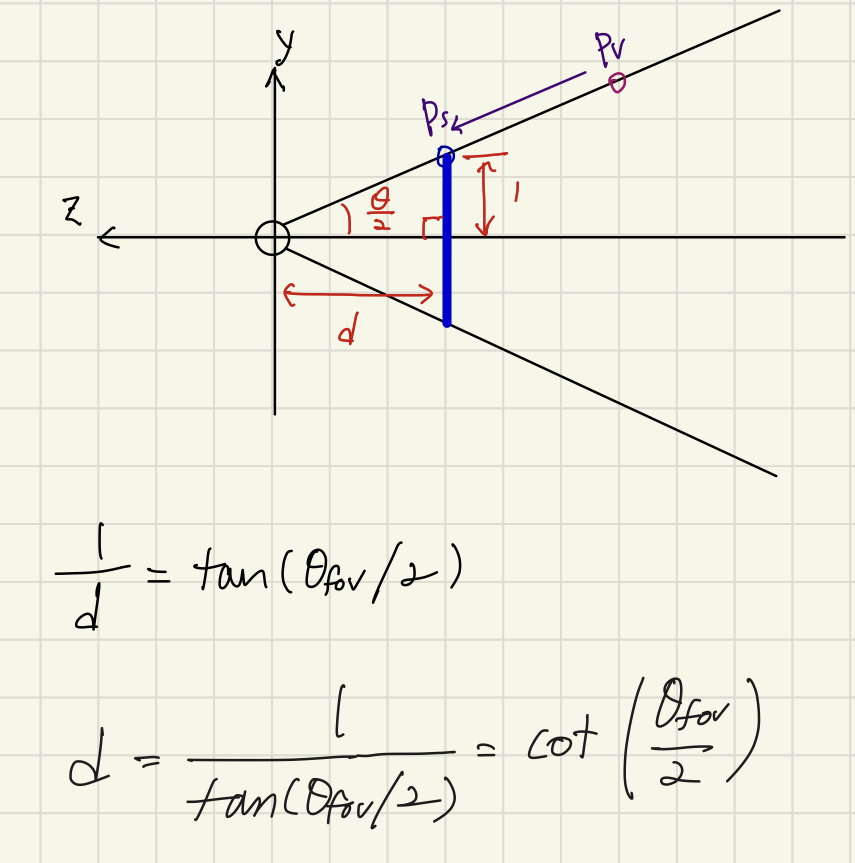
Untitled

  • 일단 단순하게 접근하기 위해서, 그림과 같이 X축은 없애고 YZ 평면만 고려하도록 하자. 이제 y와 z요소에만 신경쓰면 된다.
  • 또한 z 투영은 무시해보자. 그리고 근단면(near plane)과 원단면(far plane)도 우선 생각하지 말자. 앞서 언급한 것처럼, 원래 이론적으로 보자면 우리가 원하는 3D→2D로의 맵핑에서 z는 의미가 딱히 없다. 모든 점들이 일정한 상수 z값으로 맵핑되기 때문이다. (물론 z는 깊이 테스트 등을 이유로 나중에 쓸모가 있으므로 결국 살려두어야 한다.)
    • (참고) 프러스텀은 너무 가깝거나 너무 멀리 있는 것을 컬링하기 위해 나중에 필요하며, 프러스텀에 포함되는 점들의 z는 [-1, 1] 사이로 맵핑해줘야 한다.
  • 이제는 뷰 공간의 시야각 안에 존재하는 점들을 (x:[-1, 1] y:[-1, 1] z:-d) 인 평면 영역에 투영하는 그림이 완성되었다.
  • 결론
    • 시야각만 알면, 투영 평면까지의 거리 d를 구할 수 있으며, 그 반대도 가능하다.
    • 이게 뭐지 싶을 수도 있지만, 중요한 건 단지 하나다. 거리 d값을 먼저 구한 이유는 다음 단계에 $Y_v$에서 $Y_{ndc}$로의 변환식을 구하기 위한 것이다.

Step 2: NDC Y 구하기

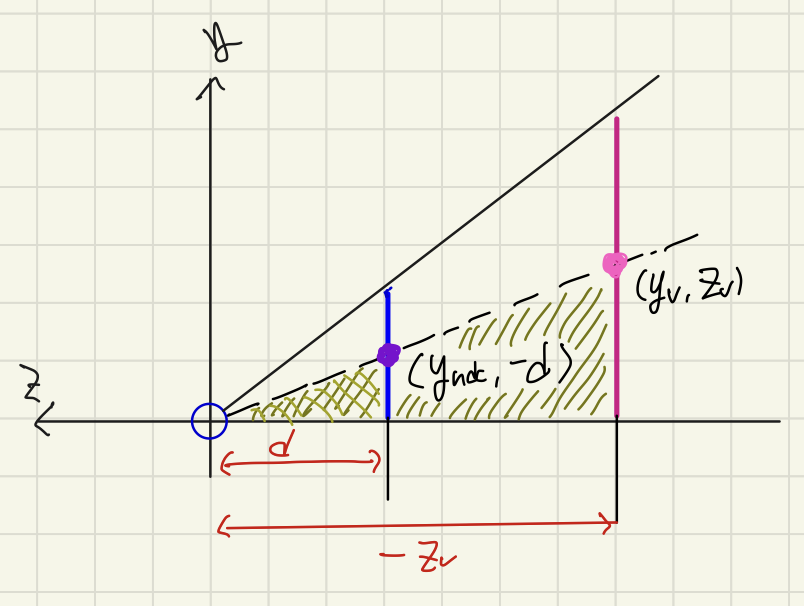
Untitled

  • 일단 앞 단계에서 거리 d값을 구해서 알고 있는 상황이다.
  • 시야 안의 임의의 점($Y_v$, $Z_v$)는 뷰 공간의 한 점으로 이미 설정해서 알고 있는 값이다.
  • 이제 시야 안에 존재하는 점($Y_v$, $Z_v$)가 ($Y_{ndc}$, $-d$)에 맵핑되고, 그 관계는 닮은꼴 삼각형 관계이므로 이것을 활용하여 $Y_{ndc}$를 구할 수 있다.

Step 3: NDC X 구하기

  • 만약에 뷰 영역이 정사각형이라면 $Xndc$도 위에서 $Yndc$를 구한 식과 같은 것을 적용하면 되겠다. 그러나 현실은 그렇지 않고 보통 가로(횡)이 세로(종)보다 큰 종횡비를 가진다. 그래서 x, y 요소 모두 동일하게 ndc 공간 [-1, 1] 영역에 맵핑하려면 종횡비를 적용해야 한다:
\[종횡비\ \ a = w / h\]
  • 더 큰 쪽이 ndc에는 빡빡하게 들어갈 것이다.

Step 4: 동차 원근 행렬 만들기 (1차)

  • NDC XY에 대한 해석
    • 둘다 $Z_v$의 나눗셈이 들어간다.
    • $Z_v$좌표로 나눗셈 연산이 들어간다는 말은 이 변환을 행렬 연산으로만 온전히 표현할 수 없다는 것을 의미한다. (변환식이 선형도 아핀도 둘 다 아니기 때문이다.)
  • 변환의 비선형적 요소를 해결할 구원투수: 동차좌표
    • 동차 공간의 w요소를 활용하자.
    • 뷰 공간의 w를 NDC 공간의 $-Z_v$로 맵핑하도록 변환식을 변형하자. 그러면 일단 나눗셈 요소는 사라질 것이다. 그리하여 이 새 변환을 적용하면, NDC 공간에서 w값이 $-Z_v$인 ndc 동차 좌표로 변환될 것이다.
    • 그 후 원본 좌표를 찾으려면 최종적으로 동차 나누기를 사용하면 된다.
    • 적어도 동차 나누기 이전의 앞부분까지는 선형 방정식으로 변환되어, 4차원 선형변환으로 우리가 쉽게 다룰 수 있게 되었다!
    • 결론
      • 원근 투영 변환은 동차 원근 행렬(4차원 선형 변환)과 동차 나누기라는 2단계로 구성된다. 먼저 뷰 공간(View Space)에서 클립 공간(Clip Space)으로 변환이 일어난다. 그 다음으로 동차 좌표를 정규화하는 과정을 거치면서 클립 공간에서 NDC 공간으로의 변환이 일어난다.

Step 5: 잊고 있던 Z - $Z_{ndc}$ 구하기

  • 지금까지는 z 변환을 고려하지 않았고 이제 z를 한번 고민해보자.
  • 앞서 구한 행렬은 가장 우측 열은 모두 0이므로 역을 가지지 않는다.
    • 한 열이 모두 0이 된다는 건 차원 하나를 잃어버리기 때문이다. (나머지 기저벡터xyz는 맵핑되지만, 마지막 기저벡터는 (0, 0, 0, 0)이 된다.)
    • 다시 말해, 뷰 공간의 점들이 ndc 공간의 단일 z평면에 맵핑되도록 식을 유도했기 때문에 발생하는 당연한 결과다.
    • 당연히 ndc공간의 점을 다시 뷰 공간으로 놓는 것도 불가능하다.
  • 그러나 우리는 Z가 필요하기 때문에 Z를 살려야 한다. 그래서 Zndc [-1, 1]로 맵핑해줘야 한다.

Step 6: 동차 원근 행렬 (2차 - 최종)

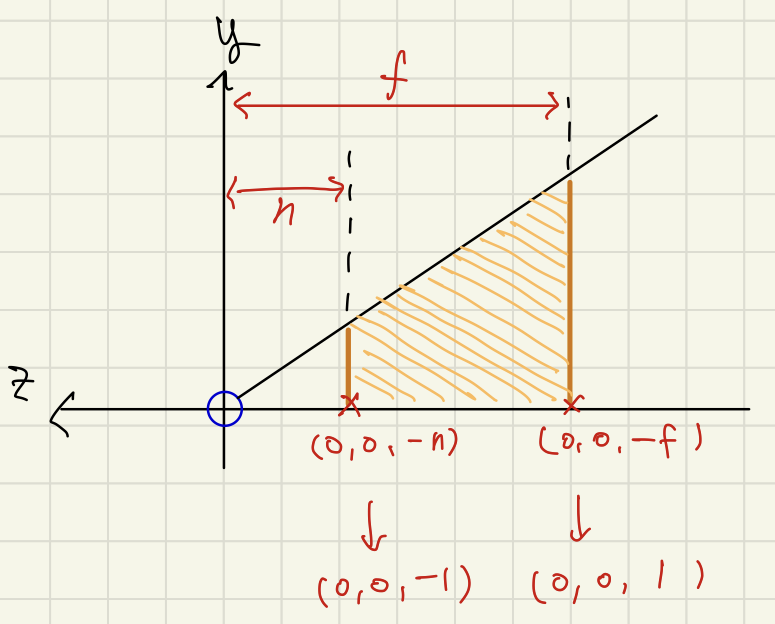
Untitled

우리는 근단면과 원단면에 해당하는 [-n, -f]를 [-1, 1]로 맵핑할 것이다.

비례 축소인자 A와 이동인자 B를 구하여 ndc 공간 z 맵핑까지 포함한 최종 NDC 변환을 완성해보자:

  • n과 f는 우리가 지정하는 값이므로 이미 알고 있는 값이다.
  • 우리는 뷰 공간 near plane 위의 점 (0, 0, -n)가 ndc 공간 (0, 0, -1)로 맵핑되어야 하는 지를 이미 알고 있다. A와 B가 포함된 변환식에 대입하여 A와 B의 관계식을 만들자. 그래서 B를 A에 관한 식으로 치환해서 없애버리자.
  • 우리는 뷰 공간 far plane 위의 점 (0, 0, -f)가 ndc 공간 (0, 0, 1)로 맵핑되어야 하는 지를 이미 알고 있다.
  • 앞서, B를 제거하고 A만 포함한 변환식에 대입하여 최종 A를 구하자.

그러면 A를 통해 B도 구하게 되고, A와 B를 채운 최종 원근 행렬을 구할 수 있다.

(참고) 여기서는 [-n, -f] → [-1, 1] 맵핑이었으나, 그래픽스 API에 따라 z 맵핑이 다를 수 있다. 당연히 행렬은 우리가 앞서 구한 것과 달라진다.

레퍼런스

van Verth, J. M., & Bishop, L. M. (2015). Essential Mathematics for Games and Interactive Applications. CRC Press.